مقاييس الانحدار لتعلم الآلة

| التصنيف | مقالات وتدوينات |
| وقت النشر |
2022/05/10
|
| الردود |
0
|
السلام عليكم ورحمة الله وبركاته
ما يتم قياسه يتحسن .....
في هذه المقالة سنرى مقاييس الانحدار الأكثر استخدامًا فهنالك العديد من المقاييس المتاحة في scikit-Learn للانحدار حيث سنرى القليل منها هنا حيث يمكننا فهم هذه المقاييس في فئتين مختلفتين وهما:
- مقاييس لقياس الأخطاء.
- المقاييس لقياس نسبة التباين الموضحة.
-مقاييس الخطأ:
تُستخدم ثلاثة مقاييس خطأ بشكل شائع لقياس الأخطاء ويشار إليها أيضًا باسم القيم المتبقية لتقييم أداء نموذج الانحدار والإبلاغ عنه:
- متوسط الخطأ المطلق (MAE)
- متوسط الخطأ التربيعي (MSE)
- جذر متوسط الخطأ التربيعي (RMSE)
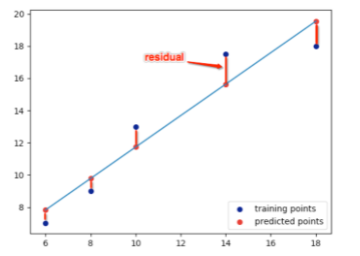 يتم الحصول على أفضل خط ملائم بتقليل البقايا فالمتبقي هو المسافة بين Y الفعلي و Y المتوقع كما هو موضح في الشكل.
يتم الحصول على أفضل خط ملائم بتقليل البقايا فالمتبقي هو المسافة بين Y الفعلي و Y المتوقع كما هو موضح في الشكل.
-متوسط الخطأ المطلق (MAE):
يقيس MAE متوسط حجم الأخطاء في مجموعة من التنبؤات دون النظر إلى اتجاهها، حيث يتم إعطاء الصيغة بواسطة، 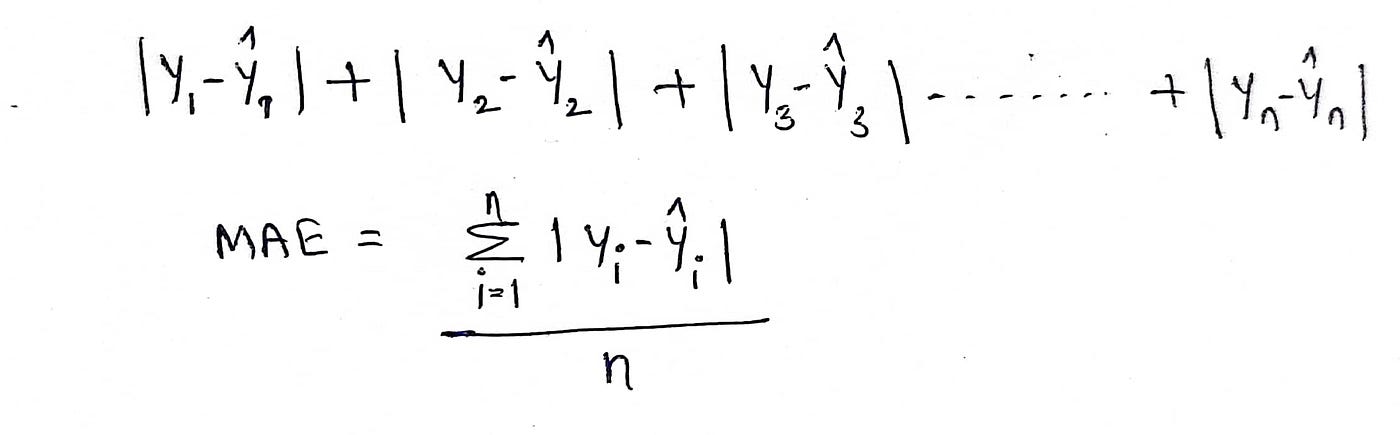 حيث:.
حيث:.
Y: باينت بيانات التدريب.
Y-hat: نقطة البيانات المتوقعة.
n: إجمالي عدد المشاهدات (الصفوف).
-مميزات MAE :
- يعبر عن متوسط خطأ تنبؤ النموذج في وحدات متغير الاهتمام بمعنى آخر يتم محاذاة MAE مع مقياس المتغير المستهدف وعلى سبيل المثال: إذا كان المتغير المستهدف في المقياس بالكيلوغرام فسيتم التعبير عن MAE بالكيلوغرام.
- MAE قوية للقيم المتطرفة.
- عيوب MAE :
- نظرًا لأن MAE تستخدم دالة المعامل وليس دالة قابلة للتفاضل والتي لا يمكن تفاضلها عند 0 فلا يمكن تطبيق تحسين الخوارزميات مثل نزول التدرج.
-متوسط الخطأ التربيعي (MSE):
يقيس MSE أو متوسط الانحراف التربيعي (MSD) لمقدر متوسط مربعات الأخطاء وحقيقة أن MSE هي دائمًا إيجابية بشكل صارم (وليست صفرية) حيث يشار إلى هذا أيضًا باسم خسارة L2 للخطأ المحسوب لملاحظة واحدة ويتم إعطاء الصيغة بواسطة،

-مميزات MSE:
- نظرًا لأن MSE عبارة عن دالة مربعة فهي قابلة للتفاضل عند 0 ويمكن تطبيق الخوارزميات المثلى مثل نزول التدرج.
- ستكون وحدات الأخطاء مربعة ويصعب تفسيرها باستخدام المتغيرات المستهدفة.
-عيوب MSE:
- ليست قوية للقيم المتطرفة.
-جذر متوسط الخطأ التربيعي (RMSE):
هو الجذر التربيعي لمتوسط مربع كل الأخطاء حيث يعد RMSE مقياسًا جيدًا للدقة ولكن فقط لمقارنة أخطاء التنبؤ الخاصة بنماذج مختلفة أو تكوينات النماذج لمتغير معين وليس بين المتغيرات لأنه يعتمد على المقياس ويتم إعطاء الصيغة بواسطة ،
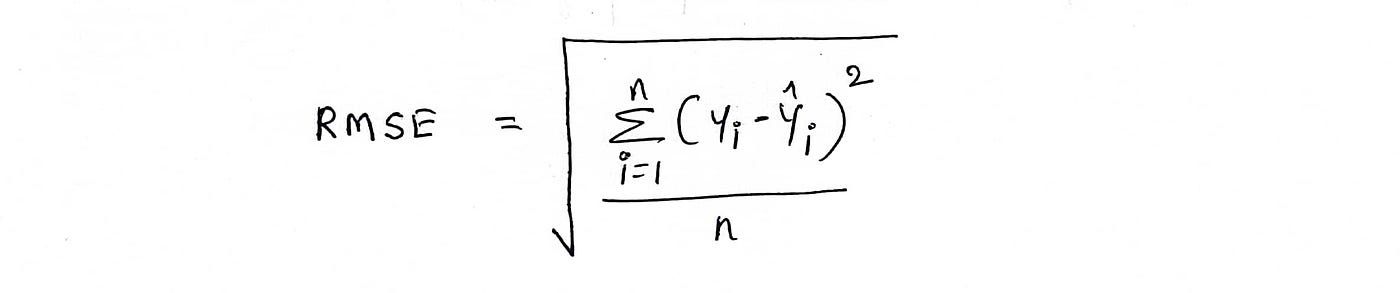
مميزاتها وعيوبها هي نفسها MAE.
-المقاييس لقياس نسبة التباين الموضحة:
-نقاط R-Squared:
هو "مقياس ملاءمة الملاءمة لنماذج الانحدار الخطي" وتشير هذه الإحصائية إلى النسبة المئوية للتباين في المتغير التابع التي تشرحها المتغيرات المستقلة بشكل جماعي حيث يُشار أيضًا إلى R-squared باسم معامل التحديد و R- تربيع الحدس الرياضي.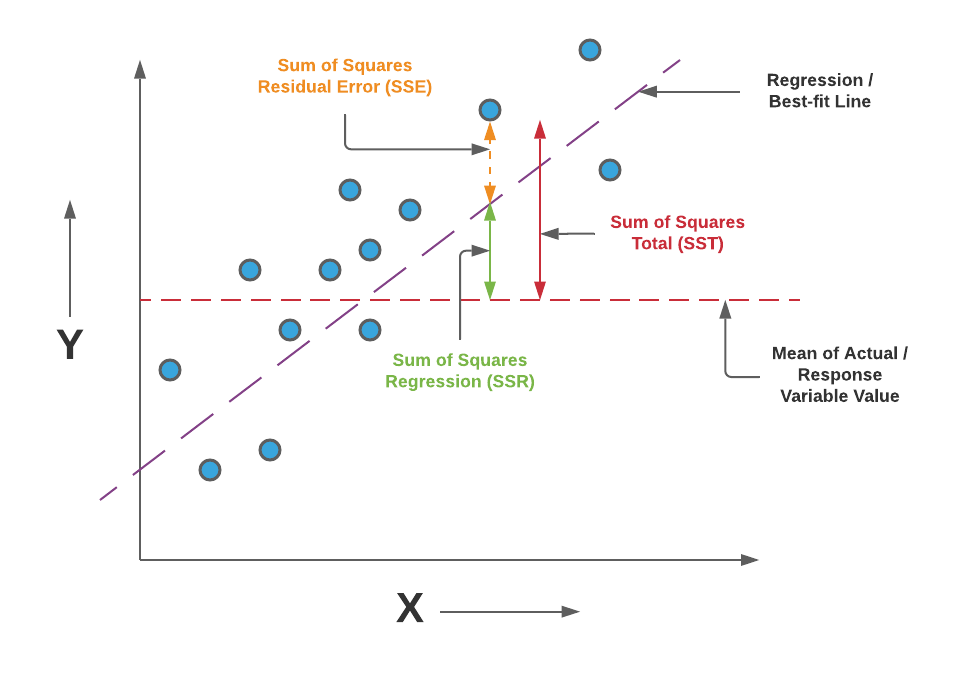
وصيغة R-squared هي،
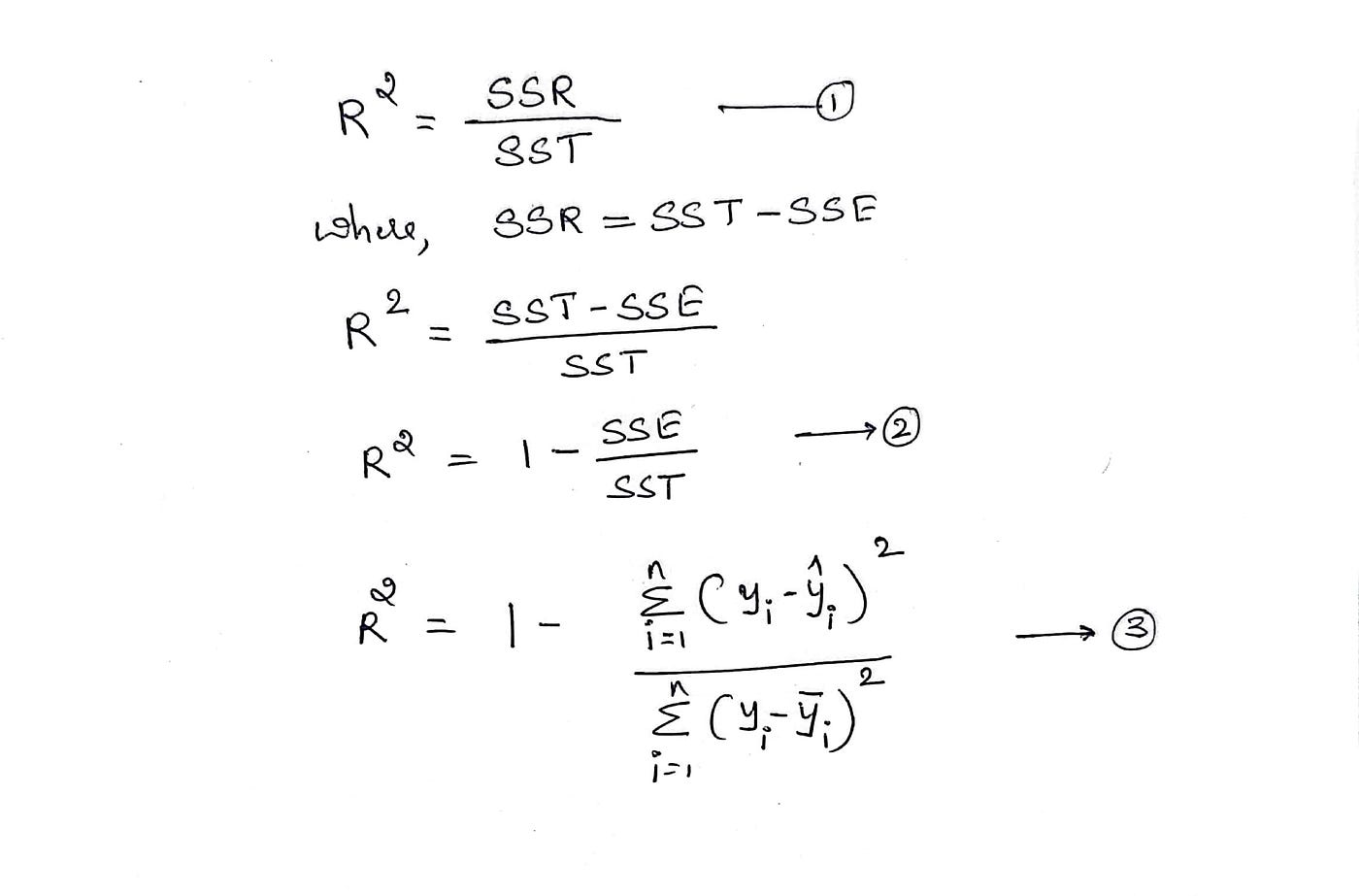
حيث يتراوح مجموع نقاط R-Squared من (0-1) وهناك حالات استثناء يمكن لـ R تربيع الانتقال إلى قيم -ve ، دعنا نرى الحالات التالية.
- R- تربيع = 0 ، هذا يعني أن خط الانحدار يمر عبر الخط المتوسط.
- R- تربيع = 1 ، هذا يعني أن خط الانحدار يمر بالضبط عبر جميع نقاط البيانات ، وهو أمر مستحيل في السيناريوهات العملية.
- R- تربيع = -ve ، يحدث هذا عندما يكون SSR أكبر من SST ، مما يعني أن خط الانحدار ينتج خطأ أكثر من الخط المتوسط ويمكن أن يكون أحد أسباب الحصول على قيم R-squared هو تطبيق الانحدار الخطي على البيانات غير الخطية للغاية.
لنفترض أنه إذا كان لدينا R-squared = 0.80 ، فسيتم قراءة هذا على أنه يتم شرح مقدار التباين لـ {المتغير التابع} بواسطة {المتغير المستقل / المتغيرات}.
-عيوب R-Squared:
- تظل درجة R التربيعية كما هي أو تزداد عند إضافة الميزة غير المهمة.
- لا تقدم معلومات حول أهمية الميزة.
- يجعل النموذج متحيزًا بسمات تافهة.
وللتغلب على العيوب المذكورة يتم إدخال تعديل R للتربيع.
-النتيجة المعدلة ل R-Squared:

حيث:.
n: إجمالي عدد المشاهدات.
k: عدد المتغيرات المستقلة (تنبؤات).
الحالة 1: إضافة عمود غير مهم عند إضافة عمود غير مهم بافتراض بقاء قيم R-Squared ثابتة حيث تنخفض قيم المقام (n-1-k ، تنخفض كلما زاد k) ويمكننا أن نرى في الشكل أدناه كيف تتأثر المصطلحات بإضافة متغيرات غير مهمة ومن ثم فإن قيمة التربيع R المعدلة تنخفض دائمًا عند إضافة متغيرات غير مهمة.
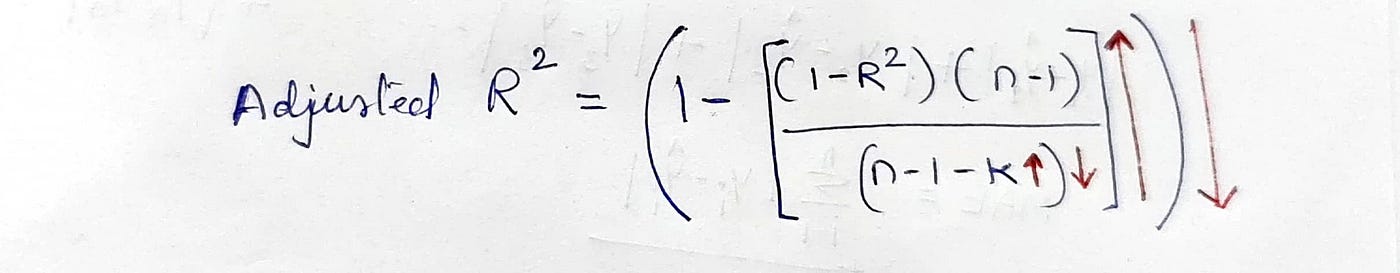
الحالة 2: إضافة عمود مهم عند إضافة عمود مهم حيث تزداد قيمة R-Squared ويمكننا أن نرى في الشكل أدناه كيف تتأثر المصطلحات بإضافة المتغيرات المهمة ومن ثم تزيد قيمة التربيع R المعدلة دائمًا عند إضافة متغيرات مهمة ويزيد مربع R المعدل عندما يحسن المصطلح الجديد النموذج أكثر مما هو متوقع بالصدفة ويتناقص عندما يقوم المتنبئ بتحسين النموذج بأقل من المتوقع. 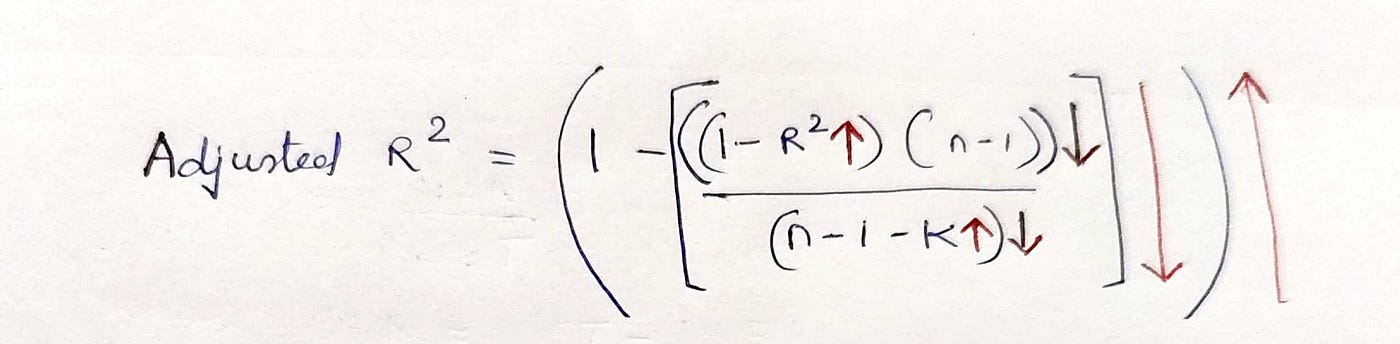
هذه المقالة ناقشت مقاييس مختلفة مستخدمة على نطاق واسع أثناء حل مشاكل الانحدار ، الخطأ التربيعي لمتوسط الجذر (RMSE) هو مصفوفة الخطأ المستخدمة على نطاق واسع في مجال التعلم العميق وكذلك التعلم الآلي ويعمل R-Squared بشكل جيد مع الانحدار الخطي البسيط ولكن عندما يتعلق الأمر بالتراجع المتعدد فإن مربع R المعدل يعطينا درجة موثوقة.
المصدر هنا.



التعليقات (0)
لم يتم إضافة ردود حتى الآن...