خوارزميات البحث

| التصنيف | مقالات وتدوينات |
| وقت النشر |
2022/06/28
|
| الردود |
0
|
السلام عليكم ورحمة الله وبركاته
في علوم الكمبيوتر تعد خوارزمية البحث خوارزمية مصممة لحل مشكلة البحث حيث تعمل خوارزميات البحث على استرداد المعلومات المخزنة ضمن بنية بيانات معينةأو محسوبة في مساحة البحث في مجال المشكلة إما بقيم منفصلة أو مستمرة، هذه المقالة ستتحدث عن خوارزميات البحث.
تم تصميم خوارزميات البحث للتحقق من عنصر أو استرداد عنصر من أي بنية بيانات حيث يتم تخزينه بناءً على نوع عملية البحث ويتم تصنيف هذه الخوارزميات عمومًا إلى فئتين:
- البحث المتسلسل: حيث يتم اجتياز القائمة أو المصفوفة بالتسلسل ويتم فحص كل عنصر على سبيل المثال: البحث الخطي.
- البحث الفاصل: تم تصميم هذه الخوارزميات خصيصًا للبحث في هياكل البيانات المصنفة ويعد هذا النوع من خوارزميات البحث أكثر فاعلية من البحث الخطي حيث يستهدف بشكل متكرر مركز بنية البحث ويقسم مساحة البحث إلى النصف فعلى سبيل المثال: بحث ثنائي.
يتم تقييم هذه الطرق بناءً على الوقت الذي تستغرقه الخوارزمية للبحث عن عنصر يطابق عنصر البحث في مجموعات البيانات ويتم تقديمها بواسطة: أفضل وقت ممكن ومتوسط الوقت وأسوأ الأوقات المخاوف الأساسية والتي توفر تنبؤات مضمونة لأداء الخوارزمية كما أنها أسهل في الحساب من متوسط الأوقات.
أنواع خوارزميات البحث:
- البحث الخطي.
- البحث الثنائي.
- البحث السريع.
- بحث الاستيفاء.
- البحث الأسي.
- بحث في قائمة فرعية (ابحث عن قائمة مرتبطة في قائمة أخرى).
- بحث Fibonacci.
- البحث الثنائي في كل مكان.
البحث الخطي:
يُعرف البحث الخطي أيضًا بالبحث المتسلسل الذي يقوم ببساطة بمسح كل عنصر في وقت واحد لنفترض أننا نريد البحث عن عنصر في مصفوفة أو قائمة ببساطة يتم حساب طوله ولا يتم القفز عند أي عنصر، لنفكر في مثال بسيط افترض أن لدينا مجموعة من 10 عناصر كما هو موضح في الشكل أدناه:
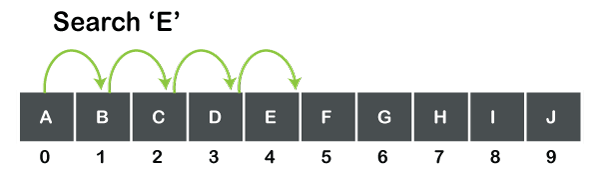
يوضح الشكل أعلاه مصفوفة من نوع الحرف تحتوي على 10 قيم فإذا أردنا البحث عن "E" فسيبدأ البحث من العنصر 0 ومسح كل عنصر حتى يتم العثور على العنصر "E" ويتم ذلك بطريقة متسلسلة من 0 حتى 4 الذي يتواجد فيه العنصر "E"، ولا يمكننا القفز مباشرة إلى 4 دون المرور ب 0,1,2,3.
البحث الثنائي:
البحث الثنائي هو بحث يتم فيه حساب العنصر الأوسط للتحقق مما إذا كان أصغر أو أكبر من العنصر المراد البحث عنه والميزة الرئيسية لاستخدام البحث الثنائي هي أنه لا يقوم بمسح كل عنصر في القائمة فبدلاً من مسح كل عنصر يقوم بالبحث في نصف القائمة لذلك يستغرق البحث الثنائي وقتًا أقل للبحث عن عنصر مقارنةً بالبحث الخطي والشرط الوحيد للبحث الثنائي هو أن المصفوفة يجب أن تكون بالترتيب الفرز بينما يعمل البحث الخطي على كل من المصفوفة المرتبة وغير المرتبة وتعتمد خوارزمية البحث الثنائي على تقنية الانقسام والقهر مما يعني أنها ستقسم المصفوفة بشكل متكرر
لفهم عمل البحث الثنائي من خلال المثال التالي:
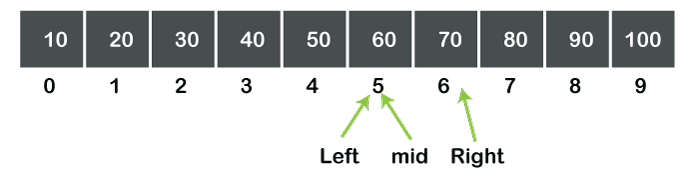
افترض أن لدينا مجموعة من 10 أحجام مفهرسة من 0 إلى 9 كما هو موضح في الشكل أدناه:
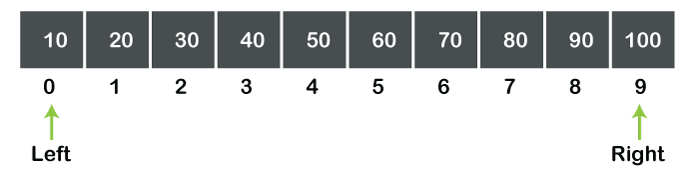
نريد البحث عن 70 عنصرًا من المصفوفة أعلاه أولاً نحسب العنصر الأوسط في المصفوفة عن طريق القانون:
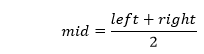
الوسط سيكون: 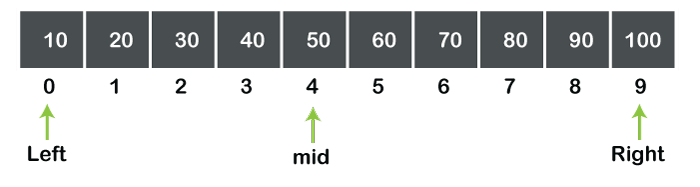
إذا لم تكن قيمة الوسط = قيمة البحث يتم النظر ليمين الوسط ويساره ونرى ما الرقم الأكبر من الذي يتم البحث عنه، ومن ثم يتم حساب قيمة الوسط من جديد، حتى نجد قيمة تساوي لما نبحث عنه.



التعليقات (0)
لم يتم إضافة ردود حتى الآن...