طريقة أشجار البحث الثنائيّة في هيكلة البيانات
| التصنيف | مقالات وتدوينات |
| وقت النشر |
2020/09/02
|
| الردود |
0
|
مقال مترجم لـ Maria Betances
تسمح أشجار البحث الثنائيّة (Binary search trees) بتخزين كميّة بيانات متغيّرة، وتسمح بتحديث هذه البيانات وفرزها بطريقة منظّمة، وللتعمّق في تفاصيل هيكلة أشجار البحث الثنائيّة وفهم العبارة السابقة جيّدًا دعنا نراجع معنى الأشجار (Trees) في هيكلة البيانات بشكلٍ سريع.
تُطلق كلمة "أشجار" على هياكل البيانات الغير خطيّة -التي يتم تنظيمها حسب العلاقات أو التسلسل الهرمي-، وهي البيانات التي تتكون من عُقَد (Nodes) وحواف (Edges)، تتصل العُقد ببعضها بواسطة الحواف، ويكون دور الحواف في تحديد العلاقة بين العُقد الأصليّة (Parent nodes) والعُقد التابعة لها (Children nodes)؛ كفكرة شجرة العائلة التي تتكوّن من الجد والأب والأبناء... وإلخ.
تُسمّى العقدة الأولى للشجرة بـ "العقدة الجذريّة (Root node)" ويمكن أن تندرج تحتها:
- عدّة عُقد.
- عقدة واحدة -عقدة فرعيّة- وتكون بمثابة العقدة الجذريّة لما يندرج تحتها، وتصبح في هذه الحالة "شجرة فرعية (Subtree)"؛ حيث يمكن أن يندرج تحتها عقدة أخرى أو عدّة عُقد أخرى.
- ومن الممكن أيضًا ألا تندرج تحتها أيُّ عُقَد، وتسمّى العُقد الأخيرة في الشجرة بـ(Leaf nodes).
ويمكنك تخيّل ذلك كشجرة تصنيف الحيوانات في علم الأحياء، أو الطريقة الشجريّة لكتابة مستندات (DOM).
ما هي الشجرة الثنائيّة؟
هناك أنواع متعدّدة من الأشجار، وهنا سنركّز على الشجرة الثنائيّة (Binary tree)، وهي هيكل بيانات يتكوّن من عُقدة أساسيّة -جذريّة- وتندرج تحتها عُقدتين كحدٍّ أقصى، ويمكن تقسيمها إلى ثلاثة أنواع:
1- ممتلئة: وهي التي تندرج تحتها عُقدتين (2 Children nodes) أو لا يندرج تحتها شيء، ولا يمكن أن تندرج تحتها عُقدة واحدة فقط.
2- المكتملة: وهي الشجرة التي تندرج عقدتان من كل عُقدة فيها إلى عُقَد المستوى الأخير التي يجب ملؤها من اليسار إلى اليمين بالترتيب.
3- المثاليّة: وهي الشجرة كاملة العُقد؛ حيث يجب أن تحتوي بالضبط على 2^(n-1) عُقدة.
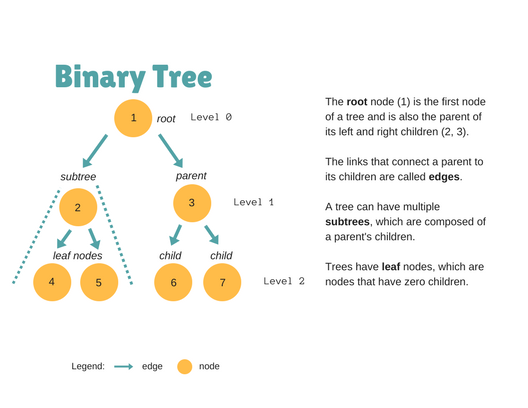
بعد أن تعرّفنا على معنى الشجرة الثنائيّة سننتقل إلى معنى "شجرة البحث الثنائيّة"... فما هي؟
تّتبِع شجرة البحث الثنائيّة أو (BST) ترتيب معيّن للعُقَد، ويتم تطبيق هذا الترتيب على جميع العُقد، ويَنُصّ الترتيب على أن جميع الاحفاد في الجهة اليُسرى أصغر من أو يساوون العُقدة n، وبنفس الوقت جميع الأحفاد بالجهة اليُمنى أكبر من العقدة n، ويمكن تبسيط العبارة بالمعادة التالية:
all left descendants <= n < all right descendants
ويعتمد تعريف العقدة -أكبر من أو أقل من- على نوع البيانات المُدخلة.
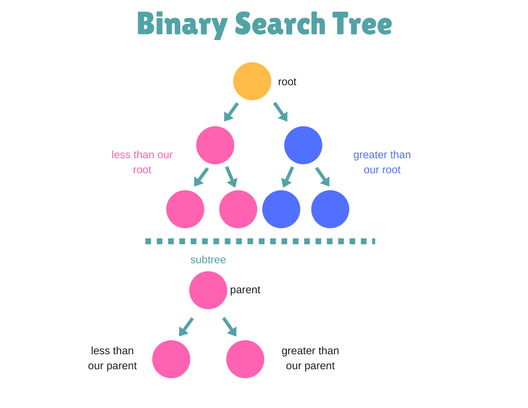
"عندما تكون أشجار البحث الثنائيّة متوازنة يصبح متوسط التعقيد الزمني للإدخال والبحث O (log n) وهذه قيمة ممتازة جدًّا"، ولفهم العبارة جيّدًا إليك الشرح التالي:
عبر تقسيم الشجرة بالمعادلة all left descendants <= n < all right descendants فإننا بذلك لا نحتاج إلى المرور بكل عُقدة في عمليّة البحث أو حتى الإدخال، لأننا قمنا بتقسيم الشجرة إلى شجرات فرعيّة (Subtrees) ستكون بيانات أحد هذه الأشجار أكبر من الأخرى، وبناءً على ذلك سنتّجه إلى فرع الشجرة الأقرب للبيانات التي بحوزتنا في عمليّة البحث أو الإدخال، وعلى سبيل المثال لو أردنا إدخال الرقم (19) في الشجرة التالية:
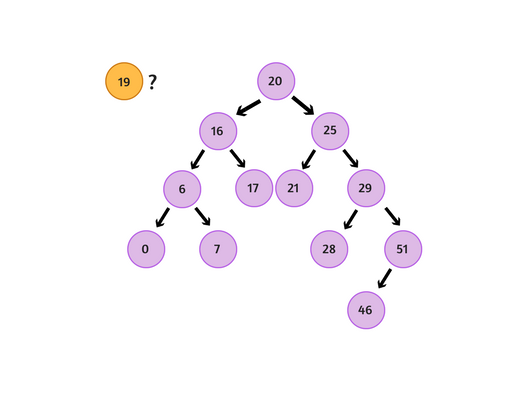
أوّلًا: سنُقارن بين الرقم 19 والرقم الموجود داخل العُقدة الجذريّة (Root node)، ولأن العدد 19 أصغر من 20 فسنتجاهل جميع العُقد الموجودة يمين العُقدة الجذريّة، وسنتّجه إلى العُقد في الجهة اليُسرى.
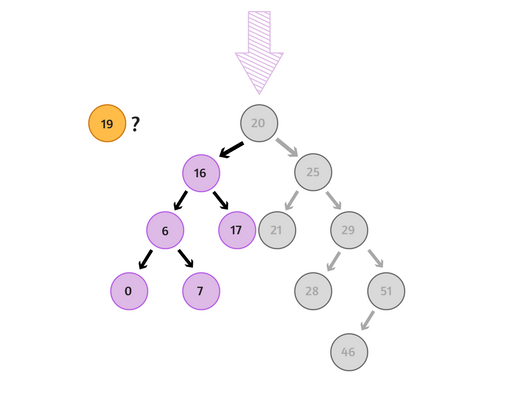
ثانيًا: سنُقارن مرةً أخرى، وسنجد أنّ العدد 19 أكبر من 16؛ وبذلك سنتجاهل جميع العُقد يسار العُقدة الفرعيّة (16):
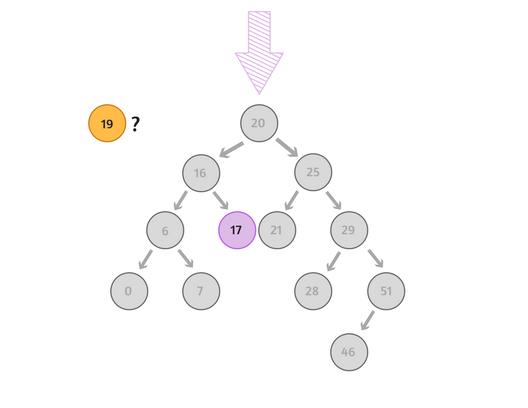
أخيرًا: العدد 19 أكبر من 17، ولا يندرج تحت العُقدة أيُّ عُقد أخرى (Children nodes)؛ ولذلك نُضيف الرقم 19 في عُقدة يمين عُقدة الرقم 17.
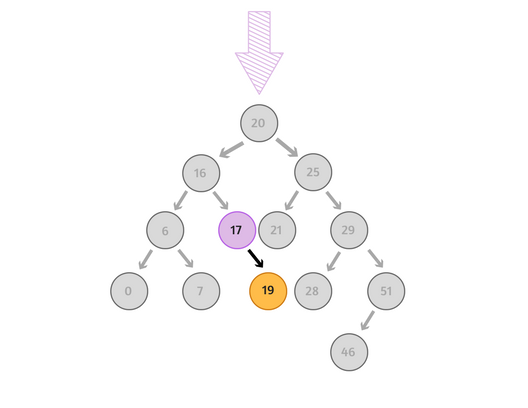
والآن... كيف سنفعل ذلك داخل البرمجيّة (الأكواد)؟
سنُنفّذ واحدةٍ بلغة JavaScript:
سنقوم ببناء شجرة البحث الثنائيّة باستخدام الـ constructor، الذي سيسهّل من عمليّة بناء العديد من شجرات البحث الثنائيّة بنفس الطريقة؛ مما سيفيدنا في عمليّة بناء الأشجار الفرعيّة.
function BinarySearchTree (val) {
this.value = val;
this.left = null;
this.right = null;
}
تأخذ الشجرة مُعامل واحد فقط (parameter) والذي سمّيناه هنا (val)، وعند استدعاؤه بمسمّاه الجديد (value) ستتكوّن لديه خاصّيتين "يُمنى ويُسرى (left وright) التي ستحتفظ بالقِيم الأكبر من العُقدة والأصغر منها.
عند إدخال عُقدة:
الآن سنعمل على طريقة بسيطة تسمح بإدخال العُقد في الشجرة، وسنفترض أنه ليس هناك أيّ قيمة مكرّرة ضمن بياناتنا.
BinarySearchTree.prototype.insert = function (value) {
let subtree = value < this.value ? 'left' : 'right';
if (this[subtree]) {
this[subtree].insert(value);
} else {
this[subtree] = new BinarySearchTree(value);
}
};
ستأخذ الـ Method قيمة الـ value كعامل مُدخل؛ وهو العامل الذي نريد تخزينه في الشجرة، ثم سنقوم بالمقارنة بين الـ value والعُقدة الحالية.
لنشرحها بمثالٍ حي:
إذا قمنا بكتابة السطر التالي:
let newTree = new BinarySearchTree(20)
في حالتنا الآن ستكون العُقدة الحالية هي نفسها العُقدة الجذريّة (Root node)،
أي أن القيمة الابتدائية لـ this.value = 20 وهي العُقدة الجذريّة
ثم إذا كتبنا السطر التالي:
newTree.insert(25)
ستكون قيمة المعامل value =25 مما يعني أنها أكبر من العُقدة الجذريّة this.value
وعند مرورنا بهذا السطر:
let subtree = value < this.value ? 'left' : 'right';
ستكون قيمة subtree = right لأن العبارة 25 < 20 خاطئة (False)
الآن سنتحقّق من الشرط الموجود داخل الـ if statement وهو this['right']، ولأن this.right = null فالشرط لا يتحقق
ولهذا سننتقل داخل الـ else وننفذ السطر الموجود داخلها
this[subtree] = new BinarySearchTree(value);
ويَبني هذا السطر "شجرة فرعيّة (Subtree)" داخل الشجرة الأساسيّة، مما يبني قيمتين يٌمنى ويٌسرى (this.left و this.right) خاصّة بالعُقدة هذه -التي تحوي الرقم 25-
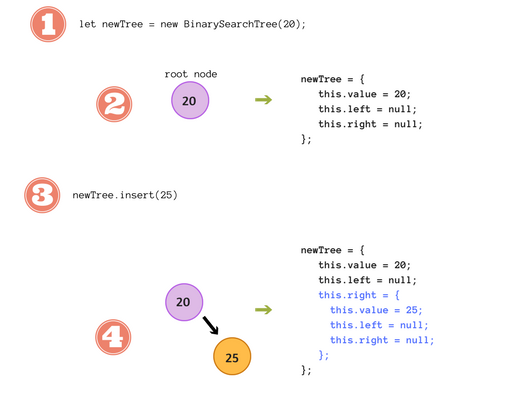
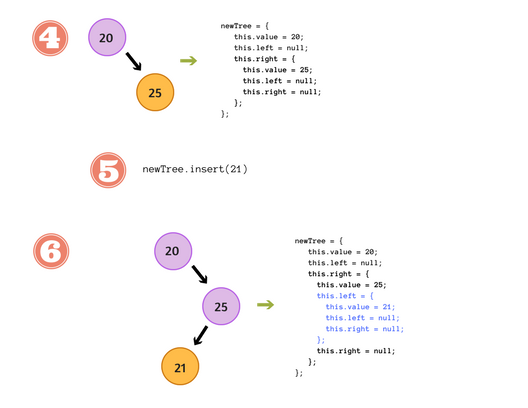
تحتوي شجرتنا الآن على عُقدتين، وسنضيف الآن عُقدة ثالثة:
newTree.insert(21)
وبتنفيذ البرمجيّة السابق شرحها سنرى أن نتيجة السطر التالي تساوي right:
let subtree = value < this.value ? 'left' : 'right';
ولذلك سيتحقّق شرط الـ if statement لأن this['right'] = true وليس null -فهي تحتوي على الرقم 25-
وبتنفيذ السطر داخل الـ if statement:
this[subtree].insert(value);
سنٌعيد استدعاء الدالة إلى أن تصبح قيمة this.right أو this.left مساوية لـ null
وستصبح كذلك حين تكون قيمة this.value = 25 و subtree = left
أي 21 < 25
عندها لن يتحقّق الشرط وسننتقل إلى الـ else
وبذلك نبني شجرة فرعيّة جديدة (this.value =21)
البحث عن عُقدة:
تشبه عمليّة البحث عن عُقدة عملية إدخالها كثيرًا، وباستخدام الـ Method التالي سنبحث عن الرقم (7):
BinarySearchTree.prototype.contains = function (value) {
if (value === this.value) {
return true;
}
let subtree = value < this.value ? 'left' : 'right';
if (this[subtree]) {
return this[subtree].contains(value);
} else {
return false;
}
};
1- سنبدأ بمقارنة القيمة المُدخلة value = 7 مع العُقدة الجذريّة التي تساوي (20).
2- إذا تساوت قيمة الرقمين سوف نُعيد القيمة المنطقيّة (true).
3- إمّا إذا لم يتساوى الرقمان فسوف نتحقّق ما إذا كانت القيمة المُدخلة value أقل من العُقدة الحالية أم لا، وعلى أساس النتيجة نُحدّد الاتجاه (right أوleft ).
4- أخيرًا...إذا وجدنا شجرة فرعيّة أخرى فسوف نُعيد الخطوة السابقة معها، أمّا إذا لم تكُن هناك شجرة فرعيّة أخرى فسوف نٌعيد القيمة المنطقيّة (false)؛ مما يعني أن الرقم غير موجود داخل الشجرة.
وبذلك شرحنا طريقتي الإدخال والبحث في شجرة البحث الثنائيّة، وعلى نمط ذلك يمكننا كتابة الـ Methods الأخرى مثل: Delete و min و max وغيرها.
يمكنك قراءة المقال الأساسي باللغة الإنجليزيّة بالضغط هنا



التعليقات (0)
لم يتم إضافة ردود حتى الآن...