ما هي المصفوفات؟ وماهي خوارزميّاتها؟
| التصنيف | مقالات وتدوينات |
| وقت النشر |
2020/09/21
|
| الردود |
0
|
تعرّف الخوارزميّة على أنّها مجموعة خطوات عمليّة لحل مشكلةٍ ما، وتُستخدم الخوارزميّات لحل مختلف أنوع المشاكل مثل: البحث عن جزء محدد من البيانات أو فرز البيانات حسب نمطٍ ما، بينما تعرّف هياكل البيانات على أنّها طريقة متّبعة لتنظيم البيانات؛ بهدف تسريع عمليّة الوصول إليها.
بمثال عملي:
- الخوارزميّات هي: (طريقة البحث الخطي والبحث الثنائي والفرز وما إلى ذلك)
- وهياكل البيانات هي: ( المصفوفات Arrays، والأشجار Trees، والقوائم المرتبطة Linked List، ويوجد العديد غيرهم)، إلا أننا سنخصّص مقالتنا هذه عن المصفوفات:
المصفوفات (Arrays)
يمكننا تشبيه المصفوفة بالصناديق المرقّمة؛ حيث يبدأ الترقيم من (0) إلى أعلى رقم (حسب عدد الصناديق)، كل صندوق ثابت في مكان حسب رقمه.
مثلًا لدينا هُنا ثلاث صناديق، إذا قمنا بترقيمها فستكون أعلى قيمة مساوية لـ (2)

1-يمكنك أن ترى محتويات أيّ صندوق بمجرد الانتقال إليه بالأمر: arrayName[2].
2-أو استبدال محتوى الصندوق بالأمر: arrayName[2]="Sherlock Holmes"، ويُستخدم هذا الامر لإضافة صندوق جديد أيضًا.
3-أمّا لإضافة صندوق جديد في آخر المصفوفة نستخدم الأمر: arrayName.push("The Memoirs of Sherlock Holmes)
كما قلنا عند استخدامك لهذا الأمر سيُضاف الصندوق في آخر المصفوفة ويأخذ الرقم التالي -label- حسب التسلسل الموجود، وفي حالتنا هذه سيأخذ الرقم (3)

4-وإذا أردت حذف الصندوق الأخير مع معرفة ما يوجد داخله -البيانات التي بداخله- فيمكنك استخدام الأمر: arrayName.pop()، هكذا دون إضافة شيء بين الأقواس، وتأكيدًا لما قلنا سترى البيانات التي بداخل الصندوق ثم سيحذفه من المصفوفة لتعود كما كانت من قبل.

5-ويمكنك استخدام الأمر: arrayName.shift() لإرسال محتويات الصندوق الأول ثم حذفه من المصفوفة، وعليك أن تعلم بأن حذف أوّل صندوق سيُعيد ترقيم الصناديق من جديد؛ حيث الصندوق رقم (1) سيصبح رقمه (0)، والصندوق رقم (2) سيصبح رقمه (1) وهكذا.
لنفترض أنك قمت بالخطوة الأخيرة -رقم 5- أي حذفت أوّل صندوق، ستصبح محتويات الصندوق رقم (1) = Sherlock Holmes، استنادًا إلى الخطوة الثانية.
6- ثم كتبت الأمر: arrayName.shift("Dr.Strange")، ستتم إضافة صندوق في أوّل المصفوفة ويكون رقمه (0)، وسيعود الصندوق الذي يحتوي على (Sherlock Holmes) إلى الرقم (2).
البحث في هياكل البيانات
البحث الخطي (Linear Search): البحث الخطي هو كالعبور على الصناديق بالترتيب من (0) إلى آخر صندوق، ورؤية ما بداخل كل صندوق إلى أن نصل إلى المحتويات التي نبحث عنها.

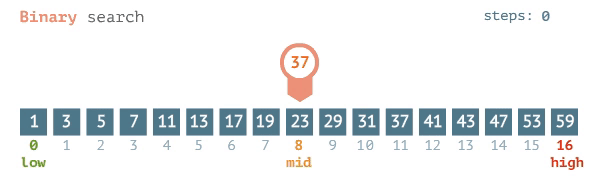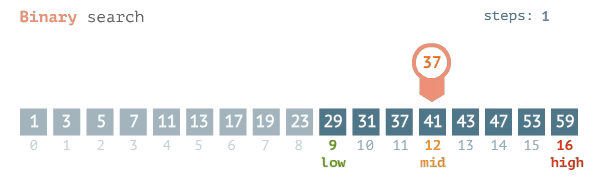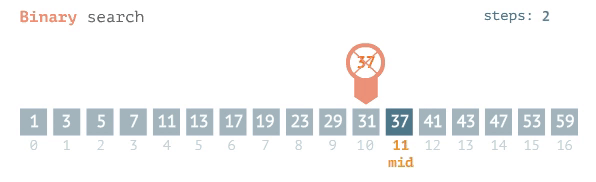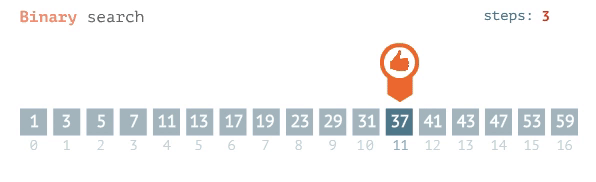
البحث الثنائي (Binary Search): يتم هذا البحث عن طريق الانتقال إلى الصندوق الذي في المنتصف والتحقّق من محتوياته، وبعد التحقّق نقرر إلى أيّ منتصف نذهب -يمين أم يسار-؟ ثم نقوم بتقسيم الجزء الذي ذهبنا إليه إلى نصفين أيضًا (عبر الانتقال إلى الصندوق الذي ينتصفهم)، وبعد التحقّق من محتوياته نقرر إلى أي جزء نذهب هذه المرة؟
للقراءة عن خوارزميّات أشجار البحث الثنائي بالتفصيل اضغط هنا
فرز هياكل البيانات
- Bubble Sort: وتعني ترتيب الصناديق من الأعلى قيمة إلى الأقل قيمة (قيمة المحتويات وليس رقم الصندوق)، فمثلًا لو كانت مصفوفتنا تتكون من 10 صناديق، سنبدأ بالصندوق رقم (0) ونقارن محتواه بمحتويات باقي الصناديق، ولنفترض أن محتوى الصندوق رقم (7) أكبر من محتوى الصندوق رقم (0)؛ إذًا سنأخذ محتويات الصندوق رقم (7) ونكمل عمليّة المقارنة من بقيّة الصناديق (8,9).
إذا كان الصندوق رقم (7) يحتوي أعلى قيمة فسيتم تخزين محتواه في الصندوق رقم (9)، وسنأخذ محتوى الصندوق رقم (9) ونُعيد مقارنته مع جميع الصناديق من (0) إلى (8)، وهكذا إلى أن يتم ترتيب قيم الصناديق تصاعديًّا "القيمة الأقل ستكون في الصندوق رقم (0)".

- Selection Sort: وتعني ترتيب الصناديق بالنظر إلى محتوى كل صندوق وتحديد الصندوق ذو القيمة الأقل، ثم نقل محتواه إلى الصندوق رقم (0)، ونقل محتوى الصندوق رقم (0) مكانه، وتكرار العمليّة؛ حيث يتم نقل محتوى الصندوق ذو القيمة الأصغر إلى الصندوق رقم (1) ونقل محتوى الصندوق رقم (1) مكانه أيضًا، وهكذا إلى أن يتم ترتيب الصناديق تصاعديًّا من الأقل قيمة إلى الأعلى.

- Insertion Sort: وتعني ترتيب الصناديق بإخراج القيمة الأولى (صندوق رقم 0) ومقارنته بالصندوق الذي يليه، ستكون لدينا أحد الحالتين:
1-إذا كان محتوى الصندوق رقم (0) أقل... تتم إعادته إلى مكانه.
2-إذا كان محتوى الصندوق رقم (0) أكبر... تتم إزاحة الصندوق رقم (1) ليصبح رقم (0)، وبالتالي سيتغيّر الصندوق رقم (0) ويصبح رقمه (1)
ثم نُعيد المقارنة بين الصندوق رقم (2) والصندوقين رقم (1) ونرى أي الحالتين السابقة سيتم تطبيقها، فإذا كانت قيمة الصندوق رقم (2) أصغر من الصندوق رقم (1) نزيح الصندوق رقم (1) ليصبح رقمه (2) ونقارن الصندوق مع رقم (0)، وتتم إضافة الصندوق ذو القيمة الأصغر في البداية.
ثم نعيد الكرة مع الصندوق رقم (3) ونقارنه مع الصناديق رقم (2) و(1) و(0)، وهكذا إلى أن ننتهي من المصفوفة.

يمكنك قراءة المقال الأصلي من هنا



التعليقات (0)
لم يتم إضافة ردود حتى الآن...